Ever wondered how increasing the number of trades in a period changes your performance? I’m really close to figuring that out to a very specifically defined calculation. The one missing variable is “correlation”. I don’t know how to account for it and how correlation impacts probability.
So for this experiment we’re going to assume binary outcomes of -100% or +250%. I’m going to assume my own variation of the kelly criterion strategy so I can model them at an equal amount of risk(?).
The logic is: If the maximum you can bet to maximize geometric growth at one single bet is 10%, then after a single bet you are left with 90% of cash. If you lose, you will be making a bet that is 9% of your initial capital anyways, so we can allocate 19% for two trades that we hold simultaneously provided there is zero correlation. If we are going to make a 3rd trade we are 81% cash so we can add an additional 8.1% risk and divide the total amount at risk by 3 and so on. It’s possible you can risk slightly more than 19% for 2 but less than 20% because a loss isn’t guarenteed. We will position as if the first position lost due to the possibility of it losing and the nature of overbetting providing less return at increased risk (where as underbetting provides less risk and return only declines slightly)
Background
For some brief background on how the risk amount to maximize growth, see the Kelly criterion. Essentially you are going to take (O1^N1)*(o2^N2) where O1 is the wealth multiplying outcome at the given position size, and N1 is the number of times you produce that outcome. For instance, at 1% position size with 250% gain and 100% loss for outcomes, O1 is 1.025 because a 1% position producing a 250% gain multiplies our wealth by 2.5% or a factor of 1.025.
This is calculated by
1+(.01*2.5)=1.025
And the loss is .99 which is calculated by
1+(.01*-1)=.99.
So for 20 wins and 30 losses the equation for how much our wealth changes is (1.025^20)(.99^30).
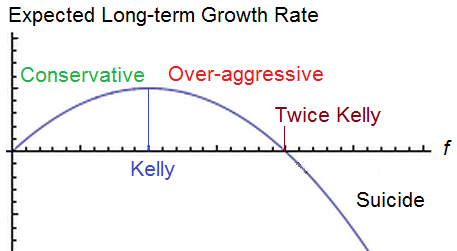
The Kelly criterion reverse engineers the position size to solve for the position size which maximizes geometric rate of return based upon your assumptions over an infinite number of bets. As volatility increases, eventually return decreases. The kelly bet seeks the point at which you can no longer improve the return without much respect for the volatility. In reality, you’d probably wish to respect a fractional kelly strategy if you want to reduce risk. It’s a good way to compare systems at an equal amount of risk. Right now I’m using a modified kelly. It is similar logic as the kelly but not the kelly exactly to increase position size based upon multiple held positions.
You could manually adjust the position size for very large outcomes with a proportional amount of wins and losses until you can’t seem to increase it to approximate the solution, or just use a kelly criterion calculator. You can run more complex calculation with more than 2 outcomes, but for now I’m just using 2.
Optimal Bet Size
So the optimal bet size for a single bet is 9% given 35% chance of a 2.5 to 1 payout.
We can then solve for the optimal bet size for 40 bets assuming zero correlation between trades but with 40 trades held during the same exact time period. There’s an important distinction here. Rather than multiplying our wealth by 1.025 with each win, at this point we are only adding 0.025 to the total portfolio per win because we don’t get the benefits of compounding when the trade is placed. Similarly, if we hold 40 1% positions at once and lose them all, we don’t lose 1-(.99^40)=.331 or 33.1% but instead lose the full 40%. So the first formula is not sufficient in describing what happens to our wealth. This is also where correlation is a bigger liability than the formula currently realizes as the chance of greater drawdowns increases as the correlation increases.
As explained before, we are going to assume a full kelly and then an additional full kelly of risk with the remaining capital for each additional bet. Since the full kelly is 9%, that means the cash on hand remaining is .91 of our portfolio which can be multiplied for each of 40 bets to determine how much cash on hand to keep
or .91^40 to equal 2.3% which leaves 97.7% at risk divided by 40 is 2.4425% per bet.
We can repeat this for 30 bets, 20 bets, 10 bets and 5 bets to construct a table of optimal bet sizes per bet.
Bet size given total number of positions.
| 50 bets | 1.98209% per bet |
| 40 bets | 2.44251% per bet |
| 30 bets | 3.13649% per bet |
| 20 bets | 4.241775% per bet |
| 10 bets | 6.105839% per bet |
| 5 bets | 7.519357% per bet |
| 1 bet | 8.9999999% per bet |
Now we can construct a simulator that sums the total % gained per bet over a period for 12 periods and randomizes the outcome according to the probability.
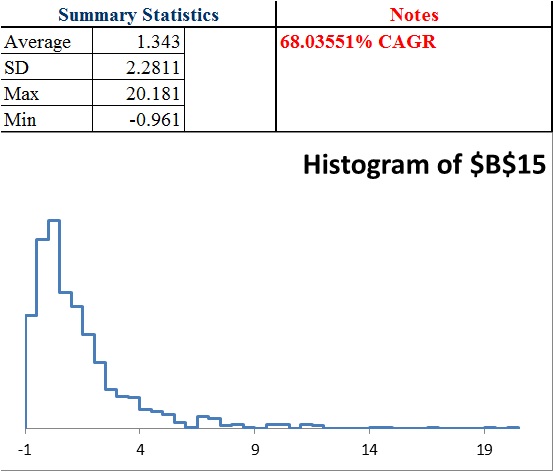
Excel gives us a function =RAND() which delivers a number between 0 and 1. If that number is less than .35 it will deliver a 2.5 times the position size outcome. If it’s more than .35 it will deliver -1 times the position size as the outcome. All position sizes for a period will be summed up and the number 1 will be added and then multiplied to the portfolio size and then the fees for the period will be subtracted. 12 periods will be simulated giving us a yearly total. We can then run through 1,000 different yearly results and see the distribution of results, the average, and even estimate the compound annual rate of return
This way we can see when the benefits of diversification outweigh the costs for smaller 5 figure portfolios where fees eat into profits. I am probably over estimating fees slightly as I used $6 per trade and assumed buys and sells for all trades, where in reality there is only an opening trade for 100% loss trades.
The CAGR is a crude estimate as the simulator only gives me the first 100 results. I am basically taking the returns plus 1 and multiplying them all and estimating X where X^100 equals 1 minus the multiple factor of the first 100 results. The CAGR will be substantially less than the mean outcome. TO illustrate imagine a 25% average return where the results are -50% of your portfolio and then +100% The actual CAGR of an equal amount of -50% returns as 100% returns would be zero, not 25%. The CAGR reflects the loss due to volatility.
I assumed a 20,000 starting portfolio and $6 fees with the assumption that there was both a buy and a sell order for each trade. Trade fees were deducted after each period’s multiplier was applied.
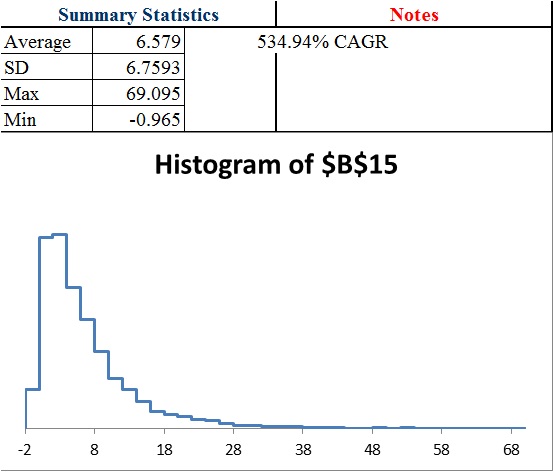
40 trades @ 2.4425% position per bet

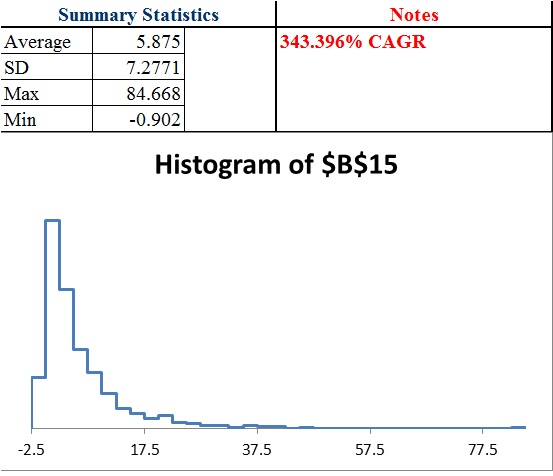
30 trades @ 3.1365% position per bet
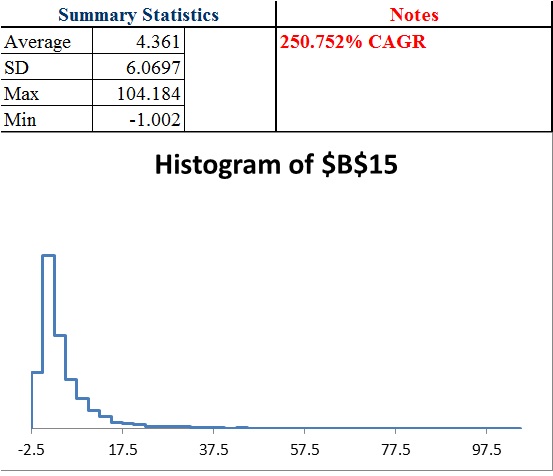
20 trades @ 4.2418% position per bet
15 trades @ 5.0466% position per bet
10 trades @ 6.1058% position per bet
5 trades @ 7.5194% position per bet
1 trade @ 9% per bet
For 12 independent trades or 1 per 1 month period, the theoretical gain is .97% growth per bet or 1.0097^12=~12.28% growth per year… theoretically. But that’s over the time horizon of infinity and as you can see by the distribution should 1,000 traders have the same exact expectation, the actual results over a year can vary wildly. Also, with only a $20,000 account taking too much risk or not enough can result in problems should losses occur early because of the size of trading fees being a flat amount.
We find we can greatly enhance the return by adding more position sizes, but the benefit of diversification decline with each additional bet.
Adjusting For Correlation
While I think the above can give you good idea for how many trades for a given portfolio size you should hold at once (and we could easily adjust the calculation for half of the initial kelly bet), we still have yet to develop a system that adjusts bet size based upon correlation. What I believe is true is that as correlation approaches one, the total amount risked should approach the single kelly bet. Afterall, if you bet all your capital on multiple trades of the same coinflip, it would be no different than betting a single bet on that coinflip. In other words in our previous example as the correlation increases the total amount at risk should approach 9%. This means that the ideal bet in reality is somewhere between the bet size calculated above at the correlation at zero (that has been calculated as shown in the prior table) and the correlation of 1 which is 9% divided by the number of bets.
For instance, if the correlation was 0.50 across 20 bets.
A correlation of zero suggests [1-(.91^20)]/20=4.241775% per bet.
A correlation of 1 suggests 9%/20=.0045 or 0.45%
Since the correlation of 0.50 is the midpoint between 0 and 1 we can average the 2 and get 2.35%*
*but that’s only an approximation.
Unfortunately the relationship may not be linear, so while we can be sure the optimal bet size for maximizing CAGR across 20 simultaneously held bets is somewhere between 0.45% and 4.241775%, we can’t be sure it is the exact average of 0.0234589 or ~2.35% per bet.
I also want to look at “half kelly” strategies in 2 different ways. One is dividing the per trade bet by 2. So for 40 bets if we calculated 2.44% the half kelly could be 1.22% per trade. That halfs the total amount of capital at risk. The other is using a 4.5% number initially, and so a 0.955^40=~15.85% cash on hand or ~84.15% invested divided by 40 or 2.10365% per trade instead of 2.44%. We can see that that is still much more aggressive than halving the amount per bet.
Normally the half kelly solution provides 3/4ths the return at 50% of the volatility of the full kelly. This is really promising for multiple bets when we can reduce the amount at risked by only a small amount and still be at an equivilent of a half kelly strategy in some regards.
In the future I also want to come up with a different calculation such as solving for the “probability of a 50% decline or more in a year” (or probability of 100% gain for example). This is pretty easy to set up.
If the result is -50% or less in a year, a simple formula will give me a 1. Otherwise zero. The average is the probability of this event. This helps you better model the probability of achieving a certain result (such as 100% return) while measuring it against a probability of a negative outcome (such as 50% loss) so you have a different way to compare risk and reward of position size and number of trades and understand expectations.
For now it seems more bets is better up to a certain point where the quality of opportunities and expectations as well as the fees become problematic. It’s hard to identify where that is, even with thousands of simulations because of the increased “skew” (the expectations become increasingly dependent upon a smaller and smaller probability of a more and more spectacular outcome) as risk and number of trades increases. Also, as your bet size decreases the aggressiveness and increases the amount of trades, the fees should become more problematic which I think we will see in a half kelly and 1/4th kelly simulation. Lowering your position below 0.50% when you have a $20,000 portfolio for example might become a problem and eat into returns too much. As such as we seek to decrease our risk, we will eventually have to decrease our number of trades or else position size will be too small given the fees to provide as big of an edge.
Comments »